NON - VIGOROUS HEADLOSS EQUATION

Wednesday, 27 May 2015 | 00:50 | 0 comment(s)

The empirical equation which are Hazen-William, Manning and Darcy Weisbach were arranged into the form of head loss equation

Darcy Weisbach

Darcy–Weisbach equation is a phenomenological equation, which relates the head loss — or pressure loss due to friction along a given length of pipe to the average velocity of the fluid flow. The equation is named after Henry Darcy and Julius Weisbach

The Darcy-Weisbach equation is valid for fully developed, steady state and incompressible flow. The friction factor or coefficient, λ -depends on the flow, if it is laminar or turbulent (the Reynolds Number) - and the roughness of the tube or duct. The friction coefficient can be calculated by using the Moody Diagram.

For this, it is necessary to substitute the following into the original head loss form of the Darcy–Weisbach equation

u^2 = \frac{Q^2}{A_w^2}

where

u is, as above, the average flow velocity
Q is the volumetric flow rate (m³/s);
A_w is the cross-sectional wetted area (m²).

For the general case of an arbitrarily-full pipe, the value of A_w will not be immediately known, being an implicit function of pipe slope, cross-sectional shape, flow rate and other variables. If, however, the pipe is assumed to be full flowing and of circular cross-section, as is common in practical scenarios, then

A_w^2 = \left(\frac{\pi D^2}{4}\right)^2 = \frac{\pi^2 D^4}{16}

where D is the diameter of the pipe

By substituting the original formulation yields the final equation for head loss in terms of volumetric flow rate in a full-flowing circular pipe. The equation below are defined.

Hazen - William

Hazen–Williams equation is an empirical relationship which relates the flow of water in a pipe with the physical properties of the pipe and the pressure drop caused by friction. It is used in the design of water pipe systems such as fire sprinkle systems, water supply networks, and irrigation systems. It is named after Allen Hazen and Gardner Stewart Williams.

The Hazen–Williams equation has the advantage that the coefficient C is not a function of the Reynold's Number, but it has the disadvantage that it is only valid for water. Also, it does not account for the temperature or viscosity of the water

The Darcy-Weisbach equation was difficult to use because the friction factor was difficult to estimate.The general form of the equation relates the mean velocity of water in a pipe with the geometric properties of the pipe and slope of the energy line.

V = k\, C\, R^{0.63}\, S^{0.54}

V is velocity
k is a conversion factor for the unit system (k = 1.318 for US customary units, k = 0.849 for SI units)
C is a roughness coefficient
R is the hydraulic radius
S is the slope of the energy line head loss per length of pipe or h_f/L

When used to calculate the head loss with the International System of Units, the equation becomes

Manning

Manning formula is also known as the Gauckler-Manning Formula or Gauckler–Manning–Strickler formula in Europe. In the United States, in practice, it is very frequently called simply Manning's Equation. The Manning formula is an empirical formula estimating the average velocity of a liquid flowing in a conduit that does not completely enclose the liquid. All flow in so-called open channels is driven by gravity. It was first presented by the French engineer Philippe Gauckler in 1867, and later re-developed by the Irish engineer Robert Manning.

The Gauckler–Manning formula states:

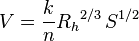
V = \frac{k}{n} {R_h}^{2/3} \, S^{1/2}

where:

V is the cross-sectional average velocity (L/T; ft/s, m/s);
n is the Gauckler–Manning coefficient. Units for values of n are often left off, however it is not dimensionless, having units of: (T/[L^1/3]; s/[ft^1/3]; s/[m^1/3]).
R_h is the hydraulic radius (L; ft, m);
S is the slope of the hydraulic grade line or the linear hydraulic head loss (L/L), which is the same as the channel bed slope when the water depth is constant. (S = h_f/L).
k is a conversion factor between SI and English units. It can be left out if consistent units are used throughout. However it is standard practice to use k=1 for SI units, and k=1.49 for English units. (Note: (1 m)^1/3/s = (3.2808399 ft) ^1/3/s = 1.4859 ft^1/3/s)

NOTE: Ks strickler = 1/n manning. The coefficient Ks strickler varies from 20 (rough stone and rough surface) to 80 m^1/3/s (smooth concrete and cast iron).

The discharge formula, Q = A V, can be used to manipulate Gauckler–Manning's equation by substitution for V. Solving for Q then allows an estimate of the volumetric flow rate(discharge) without knowing the limiting or actual flow velocity.

The equation then now is being used as a Manning headloss equation,

by : AmiraHaris

Past . Future

MechasFluid

This is all about Pipe System.